Inverse Dynamics

The ultimate aim of biomechanical analysis is to know what the muscles are doing: the timing of their contractions, the amount of force generated (or moment of force about a joint), and the power of the contraction - whether it is concentric or eccentric.

These quantities can be derived from the kinematics using the laws of physics, specifically the Newton-Euler equations:

Newton (linear): F = m.a (Force = mass x linear acceleration)

Euler (angular): M = I.a (Moment = mass moment of inertia x angular acceleration)

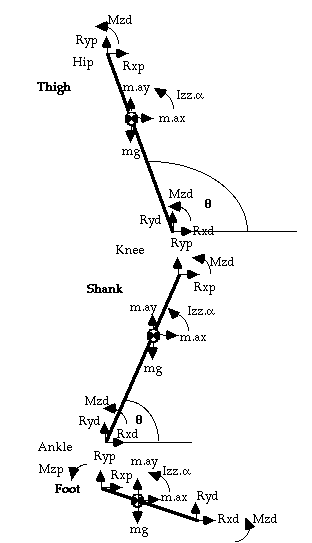
These equations describe the behaviour of a mathematical model of the limb called a link-segment model, and the process used to derive the joint moments at each joint is known as inverse dynamics, so-called because we work back from the kinematics to derive the kinetics responsible for the motion (fig. 1).

This is easily done when the motion is open-chain, with no resistance to motion at the terminal segment, since all the kinematic variables are known from motion analysis (in this case R_xd and R_yd of the first segment in the chain, the foot, are both zero). When there is contact of the limb with another object, such as the ground, or a cycle pedal, the forces between the limb and the obstructing object in this closed-chain must be measured. This is usually arranged by the technique of strain-gauging, such as used in a force platform used to measure the ground reaction force during walking and running.

Such a model is based on several assumptions, e.g.:

that the joints are frictionless pin-joints
that the segments are rigid with mass concentrated at their centres of mass
that there is no co-contraction of agonist and antagonist muscles
that air friction is minimal

Whilst these are certainly not always valid for the human body, they are nonetheless useful approximations in practice for many activities.

Joint reaction forces

from Newton, Sum of Horizontal Forces, SF_x = m.a_x:

R_xp = m.a_x - R_xd ... (1)

(where p = proximal, d = distal joint, a_y = acceleration of segment centre of mass, CoM, in y direction;

Note that d = force platform when p = ankle)

from Newton, Sum of Vertical Forces, SF_y = m.a_y:
R_yp = m.a_y + mg - R_yd ... (2)

Joint moment

about segment CoM:

from Euler, Sum of Moments, SM_z = Ia (where a = angular acceleration)

Mzp = I_z.a - M_zd - R_xp.r_p.sinq + R_yp.r_p.cosq + R_xd.r_d.sinq - R_yd.r_d.cosq

(where rp = distance from segment CoM to proximal joint) (q = angle of segment to the right-hand horizontal)

or, using motion co-ordinates (more usual),

M_zp = I_za - M_zd - Rxp.(y_p-y_CoM) + R_yp.(x_CoM-x_p) + R_xd.(y_CoM-y_d) - R_yd.(x_d-x_CoM) ... (3)

where (x_CoM, y_CoM) are the co-ordinates of the centre of mass of the segment, (x_p, y_p) the coordinates of the proximal joint (x_d, y_d) the coordinates of the distal joint

It will be noted that several body segment parameters are required to be known, such as the relative masses and mass moment of inertia (or radius of gyration) of each segment, the positions of their centres of mass. These are determined mostly from published cadaver studies, though there now exist automatic techniques for their estimation in vivo.

Segment L
(%BH) Mass (%BM)
[Dempster] Child < 14 y
Mass (kg) [Jensen] %L_CoM(%BH)
(from distal joint) Child < 14y
%L_CoM(%BH) %I *
(in kg.m²)

Head 9.6 7.8 23.8-1.14*age 50 50 49.5

Torso 31.6 46.84 42.46-0.06*age 50 40.13+0.18*age 50.3

Upper arm 16.4 2.7 0.084*age+2.2 56.4 -0.028*age+55.7 32.2

Forearm 13.7 2.3 0.015*age+1.2 55 0.19*age+56.1 30.3

Hand 8.2 0.6 50 29.7

Thigh 25.4 9.9 0.364*age+6.634 56.7 53.42+0.115*age 32.3

Shank 23.3 4.6 0.122*age+3.809 57 55.74+0.3*age 30.2

Foot 11.7 1.4 0.015*age+1.87 50 56.49+0.186*age 47.5

BM = Total Body Mass; BH = Body Height; I = %I*Segment Mass*Segment Length². Here's some slightly different ones by Plagenhoef

Muscle Moment

The moment that we obtain from inverse dynamics tells us which muscle (flexor or extensor) is active, and how much moment (torque) that muscle is exerting. A common standard method of representation of these moments in graphical form, a flexor moment (dorsiflexor at the ankle) is shown as positive, while an extensor (plantarflexor at the ankle) moment is negative.

For example, the ankle moment curve (fig. 2) indicates a negative (plantarflexor) moment throughout nearly all of stance, with a very brief and small dorsiflexor moment immediately after heel-strike. The curve tells us that the main muscle group active at the ankle throughout stance are the plantarflexors (tricpes surae), with steadily increasing activity through stance up to a maximum just before toe-off, shown in the video picture. Note that there is a range of values at each time interval - we don't all walk exactly the same! - the range shows the mean value ± 1 standard deviation of a selection of normal individuals..

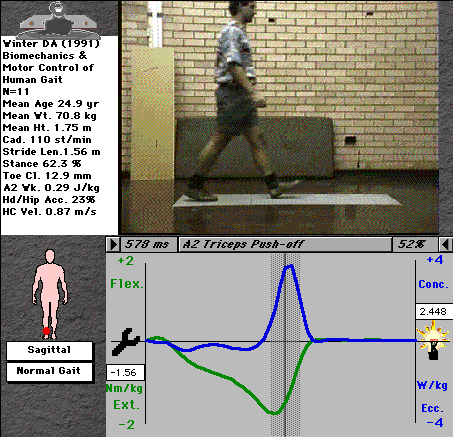
Fig. 2: Ankle moment during normal gait

Mechanical Power

Joint moment thus tells us which muscle (flexor or extensor) is contracting. It does not tell us why that muscle is contracting. For that we must look at what is termed the mechanical power. This is the joint moment multiplied by the angular velocity of the joint. So, if the joint is not moving (an isometric contraction), the angular velocity, and therefore the power, will be zero. If it is moving in the direction of the muscle contraction, the power will be positive, corresponding to concentric contraction of the muscle. If the joint is rotating away from the direction in which the muscle is pulling, the power will be negative, denoting an eccentric contraction. This is very useful, because it tells us the function of a muscle contraction: whether the muscle is being used to do external work, or to absorb energy, in effect to accelerate or brake the joint.

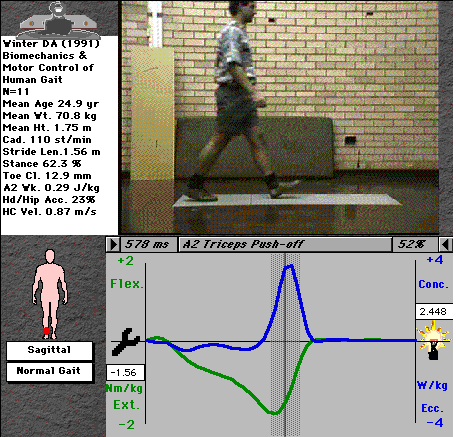
Fig. 3: Mechanical power at the ankle

Joint Activity

The moment and power curves together therefore tell us everything we need to determine the function of the musculature during a movement. It is sometimes a little difficult to look at two curves simultaneously, however. A somewhat easier method is to plot the data instead as a bar graph, with the sign indicating the moment and colour (or shading) of the bars indicating power (fig. 4):

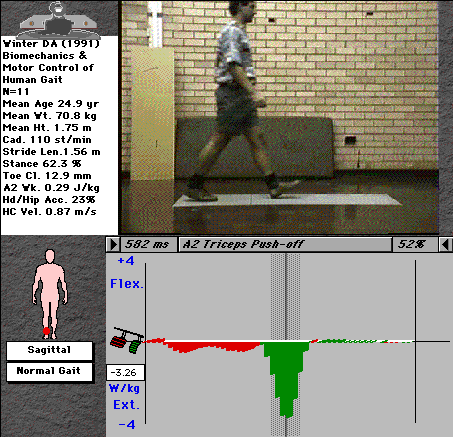
Fig. 4: Ankle joint activity

This chart shows us everything we need to know about the activity of the ankle joint musculature, clearly indicating the two distinct roles of the plantarflexors during stance. It also nicely shows the small eccentric contraction of the dorsiflexors (tibialis anterior and the peronei) immediately after heel-strike to control the foot as it lands, and their concentric contraction to lift the foot during swing.

Figs. 5 & 6 show the same plot for the knee and hip joints.

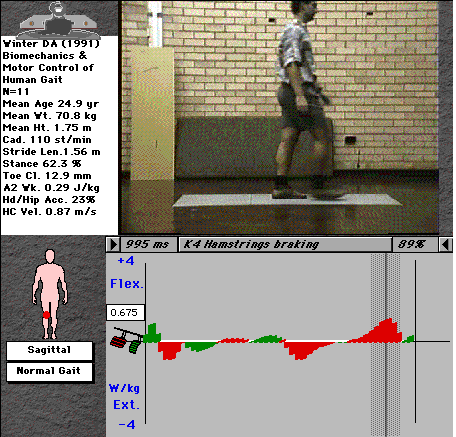
Fig. 5: Activity of the knee-joint musculature (cursor and video shown in K4 phase).

The knee shows 4 phases of distinct activity. K1 is the first eccentric phase and relates to quadriceps function during the loading response. K2 represents the same muscle group now acting concentrically to pull the trunk over the stance leg (about 10-15% of the forward energy of gait). K3 is an eccentric contraction of the quads to brace the knee against the strong contraction of the triceps (especially gastrocnemius, which tends to flex the knee as it contracts) at push-off. K4 is hamstrings braking of the leg during late swing, which increases greatly in running, when the leg swings forwards much more vigorously (with higher angular velocity).

The hip shows three rather small contractions (though there is considerable variation in hip function in normal individuals). H1 is a so-called push-from-behind caused by the gluteus maximus and hamstrings. It may contribute a small amount of forward energy, but is mainly used to stabilise the trunk at heel-strike. H2 is an eccentric burst to retard the backwards rotation of the thigh during stance, and H3 is so-called pull-off, coinciding with ankle push-off. H3 is also very much increased in running.

Limitations of Inverse Dynamics

Inverse dynamics is a very powerful technique for understanding movement, but it does have some inherent limitations:

it relies on assumptions that are not always valid - specifically:

there may be friction at the joint (e.g. in arthritis)
the distribution of mass in the segment is not uniform, and certainly not concentrated at one point

estimating the joint center of rotation is prone to error (Holden & Stanhope, 1998)

the typical models (e.g. Helen Hayes) used rely heavily on anthropometry to define the hip joint center (because it is deep and so can't be directly defined by a marker)
the joint center of rotation may also (and often does) move during motion, especially at the knee
some models (e.g. Cleveland model and six degree of freedom model used at NIH using marker triads) make less assumptions in this respect

measurement error (Holden et al, 1997)

the worst of these tends to be inaccuracies in co-alignment of the force platform and motion analysis system
best checked by a "stick" or "poker" test (Baker et al, 1997)
marker motion on the skin - especially "wand" type markers on sticks
motion at the skin-bone interface
marker tracking is sometimes contaminated by errors due to interpolation when markers go missing and data from some frames is lost

body segment parameters (anthropometry) are approximations and generalizations

very thin or overweight people, childrena and patients with wasted legs may have different proportions
note that this will mainly affect the swing phase - during stance the ground reaction forces are dominant and accelerations are minimal
special consideration must be given to amputees, in order to use values appropriate to the prosthesis components

error propagation (the errors of the distal joint calculations affect those at more proximal calculations)
it can only determine the NET moment and power

co-contraction of antagonistic muscles will cancel out - important in spastic conditions such as cerebral palsy and stroke

it cannot differentiate between different muscles

e.g. we can determine that the joint moment is flexor, but not the relative activity of each flexor muscle
for this we need electromyography (but note that this is not without its problems too!)

References

Winter DA (1991) The biomechanics and motor control of human gait: normal, elderly and pathological. University of Waterloo press, Ontario.

J.P. Holden, J.A. Orsini, K.L. Siegel, T.M. Kepple, L.H. Gerber, S.J. Stanhope, Surface movement errors in shank kinematics and
knee kinetics during gait, Gait & Posture 5 (3) (1997) pp. 217-227.

J.P. Holden, S.J. Stanhope, The effect of variation in knee center location estimates on net knee joint moments, Gait & Posture 7 (1)
(1998) pp. 1-6.

K. Manal, I. McClay, S. Stanhope, J. Richards, B. Galinat, Comparison of surface mounted markers and attachment methods in
estimating tibial rotations during walking: an in vivo study, Gait & Posture 11 (1) (2000) pp. 38 - 45.

M. Brown, S. Stanhope, Preventing Implementation And Tracking Errors From Becoming Clinical Judgement Errors In Functional
Movement Analysis, Gait & Posture 3 (2) (1995) pp. 88-88.

P.S. Fairburn, R. Palmer, J. Whybrow, S. Fielden, S. Jones, A prototype system for testing force platform dynamic performance, Gait
& Posture 12 (1) (2000) pp. 25 - 33.H.S. Gill, J.J. O'Connor, A new testing rig for force platform calibration and accuracy tests, Gait & Posture 5 (3) (1997) pp. 228-232.

R Baker, J Linskell, S Fairgrieve, M Warren-Forward, A spot check to ensure the quality of matching of kinematic and kinetic data
collected during clinical gait analysis, Gait & Posture 3 (4) (1995) pp. 282-282.

R. Baker, The _Poker_ Test: A Spot Check to confirm the accuracy of Kinetic Gait Data, Gait & Posture 5 (2) (1997) pp. 177-178.

Bobbert and Schamhardt, J. Biomechanics, v23, 7, 705-710, 1990

Jensen RK. Changes in segment inertia proportions between 4 and 20 years. J Biomech. 1989;22(6-7):529-36.

Like to know more, or criticise my methods? Email me! kirtleymd@yahoo.com

*Segment*	L *(%BH)*	*Mass (%BM)* *[Dempster]*	*Child < 14 y* *Mass (kg) [Jensen]*	*%L_CoM(%BH)* *(from distal joint)*	*Child < 14y* *%L_CoM(%BH)*	%I * *(in kg.m²)*
Head	9.6	7.8	23.8-1.14*age	50	50	49.5
Torso	31.6	46.84	42.46-0.06*age	50	40.13+0.18*age	50.3
Upper arm	16.4	2.7	0.084*age+2.2	56.4	-0.028*age+55.7	32.2
Forearm	13.7	2.3	0.015*age+1.2	55	0.19*age+56.1	30.3
Hand	8.2	0.6		50		29.7
Thigh	25.4	9.9	0.364*age+6.634	56.7	53.42+0.115*age	32.3
Shank	23.3	4.6	0.122*age+3.809	57	55.74+0.3*age	30.2
Foot	11.7	1.4	0.015*age+1.87	50	56.49+0.186*age	47.5