Forces & Moments
There are two types of force acting on the body:
Load - caused by the acceleration due to gravity (body weight)
Shear - caused by friction between the body and the ground
Load

The unit of force is the Newton (N), named after the English scientist who in 1667 discovered the famous relationship:
Force = mass x acceleration
F = m.a ... (1)
This very important equation tells us that force is proportional to acceleration. Thus the downwards force on a falling apple due to gravitational acceleration (called g, and equal to 9.81 m/s2, or approximately 10 m/s2) is:
Force = body mass x acceleration due to gravity
F = m.g
which would be, for example, 0.1 x 10 = 1 N for a typical apple with a mass of 100 grams (0.1 kg). Newton was said to have discovered the equation when he watched an apple falling off a tree.
Ground Reaction Force
When a body is not free-falling but in contact with the ground, this force is reflected back onto the body as a reaction, which is really another word for weight. Thus a typical apple experiences a reaction of 1 N. When a person stands still, this ground reaction force is equal to the person's mass multiplied by the gravitational acceleration (F = m.g). For a typical person of mass 80 kg, this reaction will be (80 x 10) 800 N. Bathroom scales measure this reaction, and the dial should really read in Newtons, but since gravity is almost constant around the world, they measure mass by dividing all the readings by 9.81 ms-2. Note that the scales would not be accurate if they were used on the moon, where gravity is about 1.6 ms-2!
Centre of Pressure
This reaction force acts upwards towards the body from all the parts of the body in contact with the ground (normally the feet). The distribution of this force (pressure) over the soles of the feet is not even, and more force is taken by some parts of the sole than others.

When all the forces over every part of the sole are averaged together, the ground reaction force can be represented by a single force acting a point called the centre of pressure (CP).
Stand still and try to feel where the centre of pressure is on the soles of your feet. Is it under the toes? Under your heels? Somewhere else? Is it the same on both sides? Try to move the centre of pressure under your toes by leaning forward and under your heels by leaning backwards (this is more tricky!). Then stand normally again and try to feel where it is.
Question: Why is it more difficult to lean backwards?
The centre of pressure must stay within the foot otherwise the body will topple over. In fact, the normal position for the centre of pressure during standing is about 5-6 cm in front of the ankle, or about half-way along the foot from heel to toes. It almost never goes behind the ankles, because the foot is "L" shaped rather than "T" shaped - there's a lot of foot in contact with the ground in front of the ankle, but only a small amount (the heel) behind. This is why you lose your balance when you try to lean backwards.
Moment of force
The fact that the ground reaction normally acts 5-6 cm in front of the ankle has big implications. Imagine two people on a see-saw, each of weight m.g Newtons:
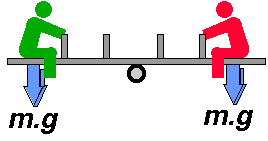
In order to balance the see-saw, the weight of each person (m.g) has to equal. What happens when one person moves closer to the fulcrum or pivot?
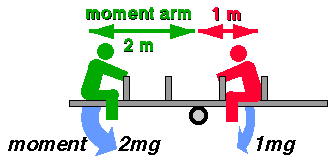
Clearly, the see-saw will tip down at the green end. The reason for this is that the turning effect of the force is dependant on the distance of the force from the pivot. This turning effect is called the moment of force (often abbreviated to "moment"), and the distance is called the moment arm (or lever arm) of the force.
The moment of the force (in units of Newton.metres, Nm) is calculated by multiplying the force (in Newtons) by the moment arm (in metres).
Ankle moment during standing

Going back to the foot during standing, we can now estimate the moment of force around the ankle joint due to the ground reaction. We saw that its magnitude was (body mass x gravitational acceleration, m.g) 800 N for a typical person of mass 80 kg. We also know that it acts at a point about 5 cm (0.05 m) in front of the ankle joint. Thus, we have:
Moment due to ground reaction = force x moment arm of force
= 800 x 0.05
= 40 Nm
Now, there must be something to balance this moment if the person is standing still, otherwise the foot would rotate about the ankle. Which way do you think it would rotate?
Remember that the ground reaction acts upwards on the body, and since it's acting on the sole at a point in front of the ankle joint, it will tend to make the foot rotate upwards (dorsiflex). What do you think is responsible for balancing the moment due to the ground reaction to keep the ankle still?
Well, there must be a moment acting in the opposite direction, tending to plantarflex the foot. Since the ankle is not at the end of its range of motion (so the ligaments are not stretched) this moment can only come from contraction of the plantarflexor muscles.
In fact, most of this moment is produced by the soleus muscle, which is one of the strongest and most fatigue-resistant muscles in the body. It has to be, because it has to produce this moment all the time we're standing, never mind walking or running! You can get an idea of how big this moment is if you hold a 4 kg mass out at arms length, since this gives a moment of force of:
Moment = weight x arm's length
= m.g.d
= 4 x 10 x 1
= 40 Nm
i.e. the same as soleus must produce during quiet standing. How does it feel? How long do you think you could hold the weight in this position?
Like to know more, or criticise my methods? Email me!  kirtley@cua.edu
kirtley@cua.edu
 kirtley@cua.edu
kirtley@cua.edu






 kirtley@cua.edu
kirtley@cua.edu