Resolution of Forces, Friction, and the ground reaction vector
Friction
So far we've looked at purely vertical forces: the force on the falling apple or the ground reaction on the body while standing still. Forces can act in other directions, though - imagine pulling a large heavy box:
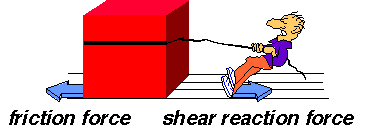
To move the box you must overcome the friction force between the box and the ground. It acts in the opposite direction to the direction you're pulling. As you pull, your ground reaction force is no longer vertical: it tilts over to produce a shear force. At first, this horizontal shear force equals the friction force on the box. As you pull harder, they both increase until eventually the friction force of the box reaches a maximum value, and the box moves.
What happens if the box is on tiles, or on ice? What if was on a deep pile carpet?
The maximum value of the friction force depends on the surface the box is sitting on. Some materials, such as ice and tiles have a very low coefficient of friction, meaning that this maximum value is relatively small, making the box easy to move. Other materials, such as carpets have much higher friction coefficients, and you must pull harder to move the box. This coefficient of friction is a number between 0 and 1, and tells us what fraction of the weight of the box must be overcome to move it. A value of 0.1 would mean that only a small force (0.1 x weight of box) would be needed to move it, while a coefficient of 0.9 would mean that a much larger force (0.9 x weight of box) is needed.
Resolution of forces
When we walk, we also produce friction forces on the ground. For example, when the foot hits the ground at heel strike, the friction between the heel and the ground causes a horizontal force to act backwards against the foot:

What will be the effect of this force on the body?
Remember Newton's equation, F = m.a? It also works for horizontal, friction forces as well as for vertical, load forces. The equation tells us that if there is a backwards force on the body, there must also be a backwards acceleration. The force therefore causes a braking action on the body, slowing it down.
What about at the end of the stance phase, at toe-off?

Here, the force is tilted over forwards, causing a forwards acceleration on the body, speeding it up into the swing phase.
Notice that the ground reaction force is not completely horizontal - it's tail is still in the air, so there must still be some vertical, load force. In fact, it's very rare to have only a vertical or a horizontal force on the body - usually they both act together as what's known as a ground reaction vector (GRV). We can see how much of each is present at any time by drawing a triangle:
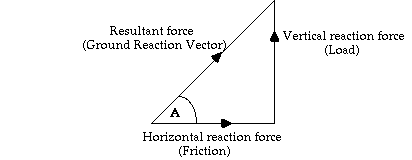
The size of the friction force is represented by the length of the horizontal line (base of the triangle), while the size of the load force is indicated by the length of the vertical line (height of the triangle). The hypotenuse of the triangle is known as the resultant force. It's size can be calculated by Pythagoras:
Resultant^2 = Load^2 + Friction^2
So, it's equal to Sqrt(Load^2 + Friction^2 ). It's direction is shown by the angle, which can be calculated by trigonometry:
tan A = opposite / adjacent = Load / Friction
This process of breaking a force down into its component parts is called resolving a force, and we will see that it can be a very powerful tool in biomechanics.
The Ground Reaction Vector in Normal Gait
We've seen that the GRV is tilted backwards at heel-strike, and forwards at toe-off. What does it do between these times?
A plot of the GRV through the gait cycle is called a butterfly diagram because the pattern made resembles the wings of a butterfly!
We can see that the vector swings round from backwards at heel-strike, vertically during the middle of stance, then forwards at toe-off. Notice that it's height changes, too. It's very small at heel-strike, rises to a maximum soon afterwards, then falls a little during the middle of stance, rises again, then falls before toe-off. This must mean that the vertical reaction force on the body also shows this pattern:
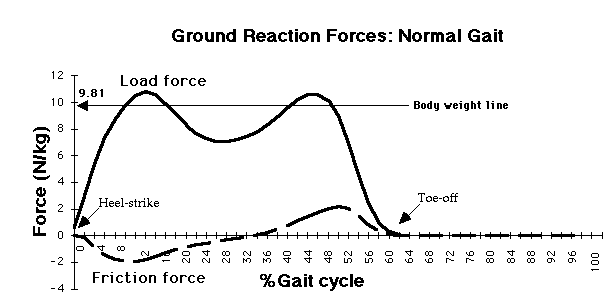
The friction force, as we saw, acts backwards (negative) after heel-strike and forwards (positive) towards toe-off. It changes at some time during the middle of stance - about 36% of the cycle.
Notice the scale on the vertical (y) axis. All the forces have been divided by body mass. This makes the graph easier to interpret for people of different body weight. It also shows one very interesting feature. One body weight would be:
body mass x gravity / body mass = gravity = 9.81 N/kg
So, we can draw a line at 9.81 to indicate body weight. We call this method of scaling the forces according to body mass normalisation, a technique which is used a lot in biomechanics. Notice that the normalised load force rises above and falls below the body weight line. What does this indicate?
Remember Newton's equation, F = m.a. The normalised vertical force on the body (in N/kg) must equal the acceleration on the body. If only gravity were acting, the force would be 9.81 N/kg. So, if it's sometimes larger or smaller than 9.81, this must mean that the acceleration on the body is sometimes larger and sometimes smaller than gravity: sometimes adding and sometimes subtracting from the downward pull of gravity:
F = mass x (gravity ± acceleration of body)
Get in a lift and press the button to go up. Feel what happens to your body weight as the lift slows down to stop (decelerating upwards = accelerating downwards). Do you feel heavier or lighter? Press to go down. How does it feel now when the lift slows down (decelerating downwards = accelerating upwards): heavier or lighter? To be really scientific, take your bathroom scales into the lift and measure the change in weight as you accelerate up and down!
Body weight increases when there is an upwards acceleration on the body, and falls when there is a downwards acceleration. In fact, NASA astronauts train for weightlessness by flying in an aeroplane while it accelerates downwards in a dive (obviously, the training sessions don't last very long!). So, in normal gait, there must be an extra upwards acceleration of the body when the load curve is above the body weight line, and an extra downwards acceleration when the load curve is below the body weight line.
Not only do we alternatively brake and accelerate while walking, we also climb and dive! In the section on kinematics, we'll see why we do this.
Reference
Winter DA (1991) The biomechanics and motor control of human gait: normal, elderly and pathological. University of Waterloo press, Ontario.
Like to add anything, or disagree? Email me!  kirtley@cua.edu
kirtley@cua.edu
 kirtley@cua.edu
kirtley@cua.edu






 kirtley@cua.edu
kirtley@cua.edu