avertical
.dt …where vvertical is the vertical velocity
of the CoM
Teach-in
2003 : Efficiency of Gait
The total
body Center of Mass (CoM) as measured by full-body 3D kinematics, shows
a typically sinusoidal pattern, with a frequency equal to the stride frequency
in the medio-lateral direction, and twice the stride frequency in the vertical
and antero-posterior directions.
Full-body 3D kinematics can be quite laborious due to the need to track many (around 30) markers. Another measurement technique uses double integration of the forces in these directions recorded from a force platform, e.g.:
avertical = Fvertical / M …where Fvertical is the vertical load and M is body mass
vvertical = avertical
.dt …where vvertical is the vertical velocity
of the CoM
dvertical = vvertical
.dt …where dvertical is the vertical
displacement of the CoM
In-shoe plantar pressure systems, such as F-Scan (Tekscan, Inc., South Boston, MA) are capable of recording the vertical ground reaction force bilaterally over many hundreds of steps. Summing the right and left forces enables the CoM to be calculated by double integration.
The resulting waveform is more or less sinusoidal, according to the subject's gait.
Since gravity acts as a downward force lifting the body up requires work to be done (or energy input). This is called potential energy (PE), and can be calculated as: PE = m.g.h
where m = mass of the object, g = gravitational acceleration (9.81 ms-2) and h is the height through which the object is raised.
Moving the body forwards also requires work to be done, in the form
of kinetic energy: KE = 0.5.m.v2
where v = the fluctuations in forward speed about the average
walking speed.
The potential
and kinetic energy curves are generally out of phase. During the rise in
the CoM, energy is converted from kinetic to potential, and then during
the fall this potential energy is converted back into kinetic energy, and
so on. The recovery rate during walking is about 65%, so only about 35%
of the energy needs to be replenished cycle (Cavagna et al, 1976).
% recovery = 100(Wv + Wf – Wext)
Wv + Wf
where Wv = vertical work per stride, Wf = forward work per stride, Wext = total external work per stride.
The % recovery depends not only on the relative magnitudes of the potential and kinetic energy curves, but also on the phase difference, a, between the time when one is at a maximum and the other at a minimum.
a = 360º. Dt
... and when a = 0º the curves are perfectly
out of phase and the gait is most efficient.
T
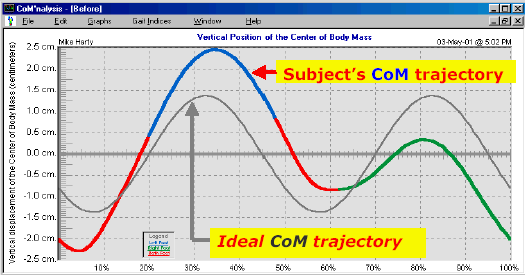
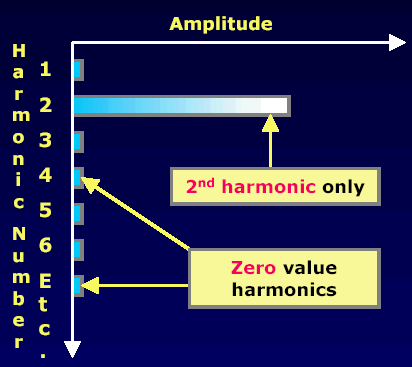
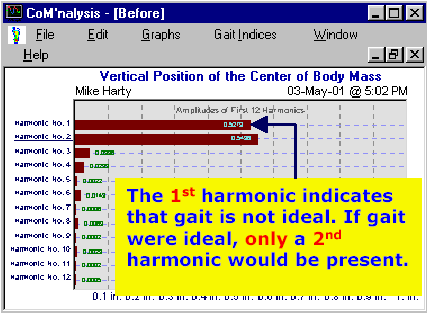
The frequency spectrum of the CoM motion can be revealed by harmonic (or Fourier analysis), converting the signal from the time to frequency domain. The most dominant frequency shows up as a large spike at a position along the horizontal axis corresponding to its frequency. Any other frequencies (called harmonics) show up as smaller peaks at different positions according to their frequency. Since there are two steps to every gait cycle, the vertical CoM trajectory has a frequency exactly twice that of the stride frequency, so the second harmonic (at twice the stride frequency) would be expected to have the largest amplitude.
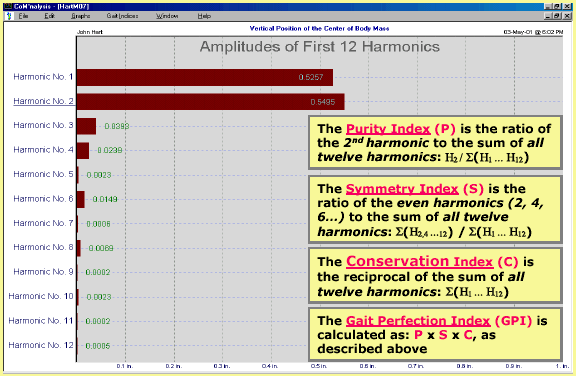
Tekscan have defined four indices of gait function:
Questions
What
we said on the CGA list
Cavagna GA, Saibene FP, Margaria R (1963) External work in walking. J. Appl. Physiol 18: 1-9.
Cavagna GA (1975) Force platforms as ergometers. J. Appl. Physiol. 39: 174-9.
Eames
MHA, Cosgrove A & Baker R. (1999) Comparing methods of estimating the
total body centre of mass in three-dimensions in normal and pathological
gaits .
Human
Movement Science 18 (5): 637-646
Hof, A.L., van der Knaap, ER, Schallig, MAA, and Struwe, DP. Calf muscle work and energy changes in human treadmill walking. J. Electromyogr. Kinesiol. 4: 203 - 216 (1993).
Minetti A. E., C. Capelli, P. Zamparo, P. E. di Prampero and F. Saibene. Effects of stride frequency changes on mechanical power and energy expenditure of walking. Med. Sci. Sports Exercise 27 (8): 1194-1202, 1995.
Murphy N (2002) Behind COM'nalysis. Technical and marketing flyer, TekScan Inc., South Boston MA.
Saina, M, Kerrigan, DC, Thirunarayan, MA, Duff-Raffaele, M. The vertical displacement of the centre of mass during walking: a comparison of four measurement methods. J Biomech Engineering. 1998; 120: 133-139.
Winter DA, Quanbury AO, Reimer GD (1976) Analysis of instantaneous energy of normal gait. J. Biomech. 9: 253-257.
Whittle MW. Three-dimensional motion of the centre of gravity of the body during walking. Human Movement Science 1997; 16: 347-355.
Back to Teach-in page