Human Motion Tracking

Statement of the Problem

By tracking the motion of body segments, a complete understanding of the kinematics and kinetics of the motion can be obtained. Traditional methods for doing this rely on tracking markers placed on the skin over bony landmarks of the segments. The problem with such techniques is that the skin moves over the underlying bone, introducing inaccuracies and noise into the measured kinematics. It also limits the application to laboratory conditions, since the markers are tedious to apply and easily come adrift during, for example, sporting motions.

What we require, therefore, is a method to track the body segments themselves, rather than applying markers to the skin. This implies tracking the contour of the limb and fitting a three-dimensional model to the observed image.

Deriving an image polygon

The first step is to use the video-image to derive an image polygon. This is done by simply scanning across the image (which has a black bacground) until a white pixel is found, then scanning across the limb until the other side is found (dark pixel):

Image...........-> Image template from threshold scan ....... -> Image polygon



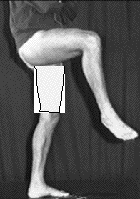
Then we derive a model template (Goncalves, Bernardo, Ursella & Perona, 1996) constructed from 10 ellipsoids strung back to back, the radii of which are defined by an anthropometry-measuring system (Baca, 1996).



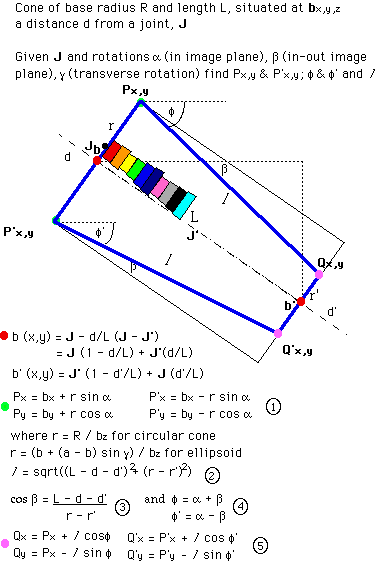
The parameters of this model (the sagittal, frontal and transverse plane angles) are set arbitrarily at first. This model polygon has a total (N) of 80 points, which more than likely is not the same as the number in the image polygon (n). So the number of points in the image is made equal by resampling it at N/n.

Matching the model and image polygons

Now the model parameters are iteratively modified until it fits closely with the image polygon. This is done by first finding a best least-squares fit of the start position of the model (which most closely matches to the image), then measuring the distance between each pair of points in each of the two polygons. The model parameters are then varied according to whether this fit is better or worse than the previous.

Like to know more, or criticise my methods? Email me! kirtley@cua.edu