
Supplied by Assistant Professor Margaret Mak, The Hong Kong Polytechnic University
Normal male subject performing a sit-to-stand activity at two different speeds (movie). The upper-limbs were held clasped against the chest, and the subject was sitting on a chair on a force platform, with his feet on another platform. The total vertical force (Fz) was recorded for both platforms.
Data was also collected by a two-dimensional Peak Performance Technologies video-based motion analysis system, and was used to determine the body centre of gravity using anthropometry from Dempster, and assuming body symmetry. Since F = ma, the vertical force should equal the vertical acceleration of the centre of gravity, plus gravity (9.81 m/s2), multiplied by body mass: F = m.(a + g).
In the curves shown below, however, there is a discrepancy in the vertical force (in Newtons) as derived by differentiation from the kinematics (red), and that measured by the force platform (blue)...

Note that for the purposes of this inverstigation, the data was not filtered, so as to exclude filtering as a cause of this discrepancy, but when filtered at 5Hz the difference between the peak forces in each case is around 50 N. When the subject was asked to stand up at a faster speed, the difference between the two curves was accentuated, with the peak force derived from kinematics some 150 N lower than that registered by the platform...
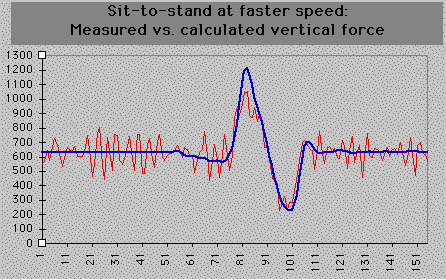
Note, however, that in both cases the baseline of the two curves are
equivalent, and that the negative-going force is faithfully recorded. The
experiments have been repeated many times with the same results.
 Questions
Questions
Conclusion
The discrepancy was caused by neglecting the head segment in the model. An abrupt downwards deceleration of the head is translated into an upwards acceleration, which is of a surprising magnitude, and nicely fills in the missing force when input to the Body CoM calculation:
![]()
Email your comments or questions to [n/a]
